About me

I am a researcher at the KU Leuven Computer Science department after obtaining a PhD at KU Leuven under supervision of Daan Huybrechs. My research is on algorithms for frame approximations and their applications.
Numerical Analysis and Applied Mathematics Section
Celestijnenlaan 200A - box 2402
B-3001 Heverlee (Leuven)
Belgium
Room : 02.49
roel.matthysen@kuleuven.be
CV
last update 05/2018
Research
My PhD research is on function approximation using frames with certain eigenvalue distributions. These arise when, for example, restricting a Fourier Basis on a rectangular domain to some smaller enclosed domain. This results in an accurate approximation of the function on the smaller domain, that is defined on the larger (and easier to work with) domain.
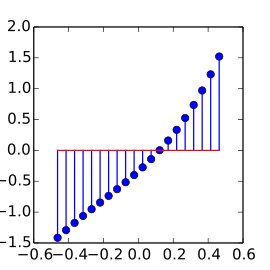
Function Values
We start from function values that are given on an equispaced grid defined on an arbitrary domain.
Example: data samples from the function $$f(x)=10e^x-17-10\cos(x-2.3)$$
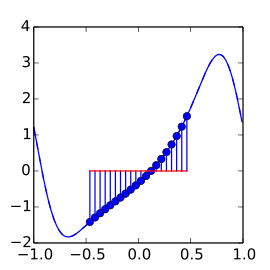
Extension
Our algorithm finds a function approximation that is periodic on some bounding box.
Example: An extension of \(f(x)\) from \([-0.5,0.5]\) to \([-1,1]\).
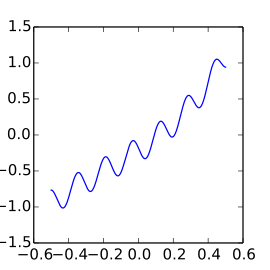
Applications
The resulting extension is used to easily solve problems such as this Helmholtz differential equation.
Example: the 1D Helmholtz equation $$\Delta p(x) + 40^2 p(x) = 1000f(x)$$ with homogeneous Neumann boundary conditions.
Software
- I am a contributor to the FrameFuns.jl, BasisFunctions.jl and Domains.jl Julia packages to compute frame approximations.
- My personal github page contains miscellaneous software projects, that may or may not be up to date.